4 August 2023

Isotope Dilution

Before introducing the age equation and how AIRIE determines geological ages, we first must explain how to determine the sample's rhenium and osmium concentration (and associated parent ¹⁸⁷Re and daughter ¹⁸⁷Os).

Introducing Isotope Dilution -- the Key to the Kingdom.

Currently, a simple instrument where an unprocessed molybdenite crystal could be dropped in, analyzed, and age determined does not exist (lucky for AIRIE). Even attempts to spot analyze molybdenite using a laser and mass spectrometer (LA-ICP-MS) does not yield acceptably precise ages. To get the high precision AIRIE achieves for molybdenite model ages and isochron ages for other geologic material (sulfides, organic shales, bitumen), isotope dilution must be employed.

As described in the prior blog post, isotopes are atomic configurations of an element with differing number of neutrons in the nucleus leading to different atomic masses. Isotopes can be stable or radioactive and the relative amount of isotopes is the element's isotopic composition. Isotope dilution analysis determines the amount of an isotope by mixing the unknown sample with a solution of known characteristics (concentration and isotopic composition). The solution of known, calibrated concentration and isotopic composition is called a spike or tracer.

In equation form it looks like: 
and rearranging the formula yields: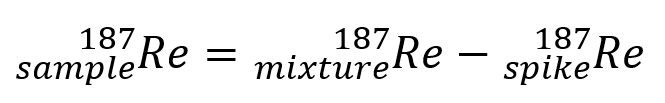 
Yet again, instrumentation able to directly measure the spike-sample mixture is also too imprecise for the high precision geochronology AIRIE promotes. But, mass spectrometers are very adept at measuring ratios of isotopes, so if both the sample and the spike solution have multiple isotopes AND the relative ratios of the isotopes in question are notably different, then it is possible to solve the isotope dilution equation for the amount of isotope in question.

The equation becomes: 
With algebraic manipulation and use of known isotopic ratio constants, the equation can be rearranged to (see full proof here): 
There are requirements that must be met in order to use isotope dilution: 1) both the concentration and isotopic composition of the tracer must be well known and the isotopic composition must be distinctly different from the sample, 2) the sample and tracer must be chemically equilibrated prior to any processing or measurement, 3) any processing or measuring of the mixture must either a) not fractionate (or change) the mixture's isotopic ratio or b) account and correct for any fractionation.

A key criterion for high quality isotope dilution determination is creating a spike-sample mixture of ideal proportions. Too little spike and the sample contribution will swamp the mixture and vice versa. When this occurs, the calculated value becomes highly sensitive to the measured ratio, which, by its very nature, is variable. We measure using procedures known to produce the most accurate value, but there is always scatter associated with the measurement (which is wholly accounted for during error propagation).

Think of two jars, one with 500 black and 500 while balls and the other with 50 black and 950 white balls. If you randomly grab 50 balls from each jar, the ratio of white:black in the handful from the first jar is likely close to the 1:1 of the jar whereas the ratio from the second jar may or may not be close to the 1:19 of the jar. Do this multiple times and the variability of the ratio from the first jar is likely to remain low with most handfuls close to 1:1 whereas the variability of the ratio in the handful from the second jar may be very high.

Actual spike-sample mixtures measured at AIRIE are similar so when a sample is described as over- or under-spiked, it implies our approximation of sample concentration was incorrect. By default, AIRIE will re-analyze the sample using the newly determined (albeit less precisely known) concentration to achieve ideal spike-sample proportions. Overall, we find that samples re-analyzed show only marginal changes in absolute concentration (and age) but marked improvement in precision when spiked optimally.

And that is Isotope Dilution. Now that we know how to determine the concentration of parent and daughter isotopes in a sample, we can determine the sample age, which will be discussed in our next blog post.