5 September 2024

The Age Equation and Model Ages

Radioactive decay was discussed in one of our first blog posts. To summarize, decay is the spontaneous reconfiguration of an atom's nucleus to arrive at a more stable energy state. Given enough time, the decay occurs at a statistically constant rate and is defined as the decay constant (lambda, l).

So a pile of radioactive atoms, say ¹⁸⁷Re, will decay to ¹⁸⁷Os via beta decay at a rate of 1.666x10^-11 per year. The actual amount of ¹⁸⁷Os produced is directly proportional to 1.) the amount of ¹⁸⁷Re and 2.) time elapsed.

In mathematical terms, the change in atoms, dN, over a change in time, dt, is proportional to initial atoms, N_o, and the decay rate, l. This is a partial differential equation which you can solve using t=0 => N=N_o as a boundary condition to get N = N_o * e^-lt. Finally, we know that N_o equals the amount of present day parent isotope (P) plus present day daughter isotope (D) given the decay is 1:1 (and we are not accounting for initial daughter, yet...).

Put all this information together, assign parent, P, to ¹⁸⁷Re and daughter, D, to ¹⁸⁷Os, the equation presented on the blog page is determined: ¹⁸⁷Os = ¹⁸⁷Re * (e^lt - 1). This is the "model" age equation because it only accounts for radioactive decay and does not account for any daughter isotope present at the start of decay (usually crystallization with consideration for cooling closure temperatures that restrict atomic mobility within the system).

And, as you may have read in our Isotope Dilution blog post, we can determine present day ¹⁸⁷Re and ¹⁸⁷Os (along with the other Os isotopes) at AIRIE and therefore calculate a sample's geologic model age.

The beauty of molybdenite, and other so-called "Low Level, Highly Radiogenic" (LLHR) samples is the amount of initial ¹⁸⁷Os is vanishingly small relative to the amount of decay-produced ¹⁸⁷Os as Re readily substitutes for Mo in the molybdenite, MoS₂, crystal structure and Os does not.

For example, take 20 milligrams (20 mg) of molybdenite from a molybdenite-quartz vein from a Cu-Mo porphyry deposit in Chile that is 72 million years old (72 Ma). Typically, the molybdenite contains 100 parts per million (100 ppm) rhenium and 0.2 parts per billion (0.2 ppb) Os with a low ¹⁸⁷Os/¹⁸⁸Os since the metals were sourced from a mantle-like reservoir.

Using the isotopic composition of the Re and Os, the sample weight, the concentration of Re and Os, and the age, you can calculate ~1252 nanomoles (1252 nMol) ¹⁸⁷Re produced ~1.50 nMol ¹⁸⁷Os whereas only 0.00011 nMol ¹⁸⁷Os were present at t = 0. Looking at the table below, see how the age changes with varying amounts of initial Os, from 0 to 20 ppb (which would be extreme common Os enrichment in molybdenite).


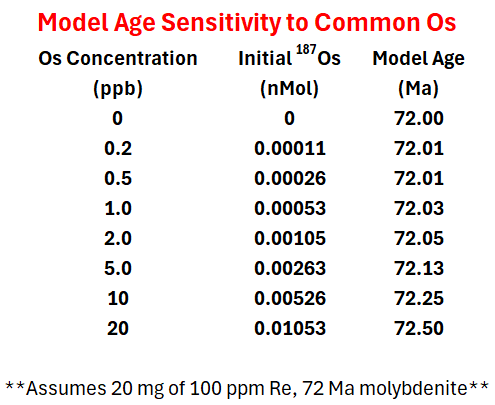
The age changes by less than 1% when the Os is increased 100X! Even more importantly, at AIRIE, we quantify the initial Os present and account for initial ¹⁸⁷Os in order to not assume it is 0 or some other value. The only problem is analytically, it is hard to quantitatively determine the common Os when the radiogenic ¹⁸⁷Os is so large and we optimize our spike-sample ratio to best determine radiogenic ¹⁸⁷Os. Nonetheless, our data reduction procedure removes initial ¹⁸⁷Os resulting in the most robust, accurate model ages possible. We report all this information in our publication-ready data tables such as the one shown below (see highlights).

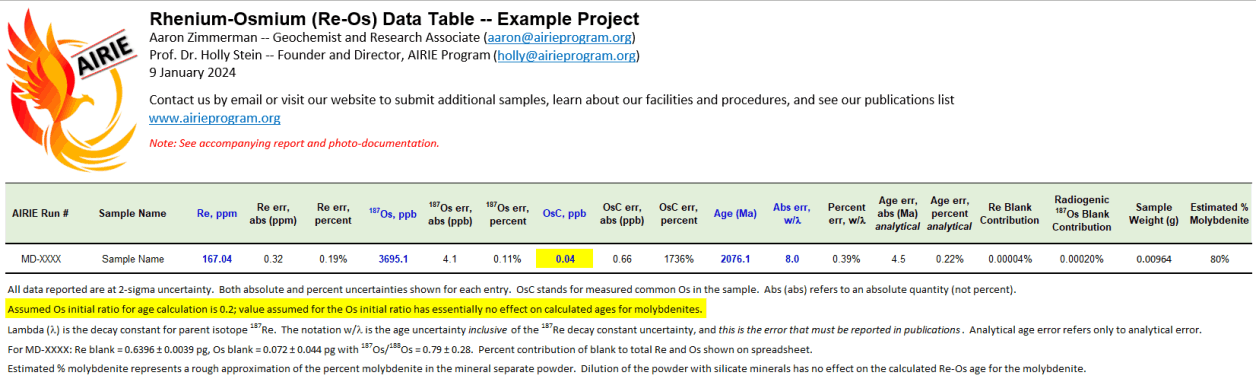
To summarize, radioactive decay produces daughter isotopes over time proportional to the amount of parent present at time = 0. Via isotope dilution, we accurately determine the present day parent and daughter concentration in a sample and also attempt to determine the amount of initial daughter isotope. When the radioactive daughter is demonstrably larger than the initial daughter product, a model age is calculated and is robust across a broad swath of assumptions for the system at the starting time.